by Ben Evans, CFD Engineer & Aerodynamicist – BLOODHOUND aerodynamics

BLOODHOUND SSC will be the first – and, probably for a long time, the only – land-based vehicle in history to travel for a sustained period of time well above the speed of sound. Hence one of the crucial aspects of the aerodynamics of the Car is unique, and that’s the supersonic nature of the air flow, and in particular the presence of shock waves and their interaction with the ground.

Shock waves on a supersonic vehicle

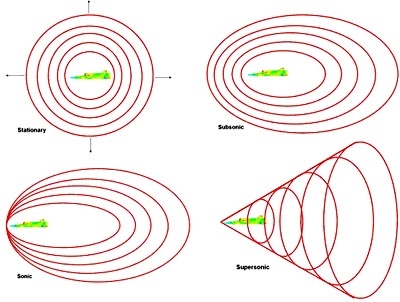Shock waves form because of the nature of the propagation of sound waves through the air.

Under normal subsonic conditions, any body, whether it be a jogger or Formula 1 car, transmits pressure disturbances ahead of it in the form of sound waves. These waves carry the ‘information’ to the air molecules ahead of it so they have advance warning that the body is coming and that they need to start moving out of the way. However, when the body itself is travelling at the same speed (sonic) or faster (supersonic) than the speed of these sound waves, it can no longer transmit this information forward and the waves ‘bunch up’ right in front of the vehicle forming a shock wave which we experience in the form of an audible ‘sonic boom’.

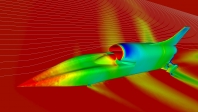
When this happens, the flow properties (for example pressure and density) around the vehicle no longer vary smoothly but change rapidly at the shock waves. You can see this in the picture at the top of this page which simulates the pressure contours over one of the early BLOODHOUND designs travelling at Mach 1.3 (that is 1.3 times the speed of sound).

Understanding how these shock waves interact with the Car and with the desert surface has therefore been a crucial part of the aerodynamic research for the BLOODHOUND programme.

Why model aerodynamic behaviour?

The aerodynamic behaviour of individual components of the Car has been studied in conjunction with studies of the vehicle as a whole.

Modelling the flow around the base of the wheels under various configurations, for example, was very important in letting us understand how they will interact with the desert surface. The overall dimensions of the wheel had been fixed, at the outset, by structural integrity specifications. So we then applied aerodynamic considerations to design of the finer detail of the wheel profile which resulted in the typical flow patterns around the base of the front wheels shown in figure 3.

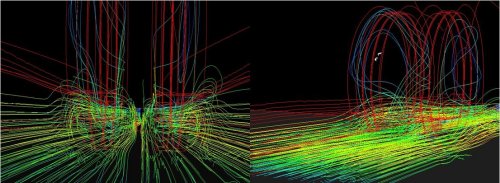
Figure 3: Flow patterns around the ‘side-by-side’ front wheel configuration

Obviously, analysing standalone components, such as the jet intake duct or winglets, in isolation has its merits. However, it is not until all of these components are put together and we analyse the full vehicle aerodynamic behaviour that we can understand how these components interact with each other aerodynamically.

Does pitch matter?

In addition to determining the variation in the lift and drag coefficients for the vehicle over the Mach range in its design configuration, we also need to understand how the Car will respond aerodynamically as a function of yaw, pitch (angle of attack) and ride height as these will all be variables on an actual run of the Car.

You can see the effect of pitch angle on lift for one of the early BLOODHOUND concepts in figure 4. This graph indicates that the slender shape of BLOODHOUND is relatively insensitive to pitch angle over the range that it is likely to be experiencing during desert runs (ie the lift against pitch curves are not too steep). What that means is that the effect of the vehicle’s pitch has a relatively small effect on its lift, in comparison with a wing, for example. This is an important property as far as stability – and, therefore, safety – of the Car is concerned.

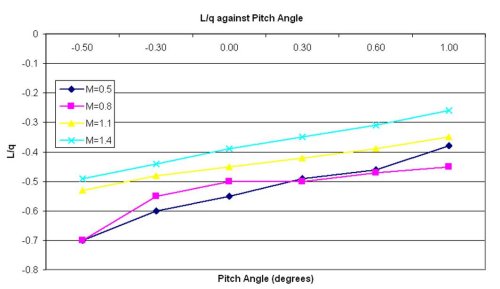
Figure 4: Effect of vehicle pitch angle on lift

Does ride height matter?

Figure 5 shows the effect of vehicle ride height on lift and drag. The drag is insensitive to ride height, but a lower ride height generates an increase in download over the vehicle. This can be explained quite simply by using Bernoulli’s famous theorem, which states that, due to the principle of conservation of energy, the total energy of a lump of fluid moving with the flow must remain constant.

If compressibility of the air effects are ignored, this implies that as the fluid accelerates to pass through the tight space under the Car, the corresponding increase in kinetic energy must be compensated for by a decrease in some other form of energy – in this case it's pressure.

The implication is that the closer the Car is to the ground:

• the faster the flow must accelerate to ‘squeeze’ underneath the Car
• and hence the pressure experienced by the base of the car is lower
• and therefore the suction effect pulling it towards the ground is greater.

At 1,000mph we can generate huge forces, which means that although a bit of download is good, too much is not, so we used this data to find the ideal ride height.

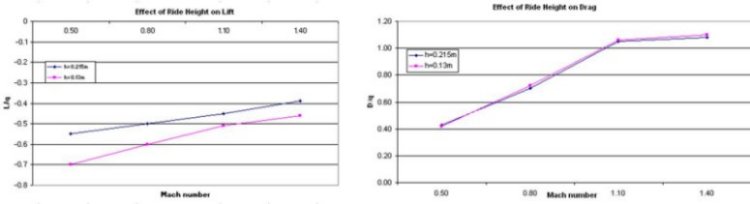
Figure 5: Effect of vehicle ride height on lift and drag

Although BLOODHOUND is designed to have a maximum speed of 1,050mph, the aerodynamic response of the car has to be such that it is safe and drivable all the way from its initial roll forward up to this top speed. This makes optimising the geometry of the design an extremely complex activity. And it's even more challenging because the Car accelerates and decelerates through the ‘transonic’ regime (just below fully supersonic) when parts of the flow field are still supersonic and parts remain subsonic, and conditions (such as positions of shock waves) are changing rapidly.

All in all, this makes working on the aerodynamics of BLOODHOUND both a massive privilege and a massive challenge!